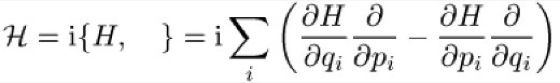Satz von Liouville (Physik)

Der Satz von Liouville (auch Liouville-Theorem genannt, nach Joseph Liouville) ist ein Satz aus dem Bereich der theoretischen Mechanik, der besagt, dass das von benachbarten Trajektorien im Phasenraum eingeschlossene (mehrdimensionale) Volumen als Funktion der Zeit konstant ist. Der Satz gilt für alle durch den Hamilton-Formalismus beschriebenen Systeme. Die Hamilton-Funktion kann dabei auch explizit von der Zeit abhängen. Eng verwandt mit dem Satz von Liouville und leicht daraus herleitbar ist die Liouville-Gleichung.

Herleitung

Im Rahmen des Hamilton-Formalismus ist der momentane Zustand eines mechanischen Systems gegeben durch kanonische Koordinaten ${\displaystyle q_{i}}$ und kanonische Impulse ${\displaystyle p_{i}}$ mit ${\displaystyle 1\leq i\leq N}$, d. h. durch einen Punkt ${\displaystyle X=(q_{i},p_{i})}$ im Phasenraum. Die Hamilton-Funktion ${\displaystyle H(q,p,t)}$ des Systems definiert ein Vektorfeld ${\displaystyle {\dot {X}}=\left({\frac {\mathrm {d} q_{i}}{\mathrm {d} t}},{\frac {\mathrm {d} p_{i}}{\mathrm {d} t}}\right)=\left({\frac {\partial H}{\partial p_{i}}},-{\frac {\partial H}{\partial q_{i}}}\right)}$ im Phasenraum, welches die Zeitentwicklung des Systems beschreibt. Die Lösung der Gleichung ist der Fluss ${\displaystyle X(t)}$. Anwenden des Divergenzoperators ${\displaystyle \operatorname {div} =\left({\frac {\partial }{\partial q_{i}}},{\frac {\partial }{\partial p_{i}}}\right)}$ auf das Vektorfeld liefert

${\displaystyle \operatorname {div} \cdot {\dot {X}}=\sum _{i=1}^{N}\left({\frac {\partial ^{2}H}{\partial p_{i}\partial q_{i}}}-{\frac {\partial ^{2}H}{\partial q_{i}\partial p_{i}}}\right)=0.}$

Das Geschwindigkeitsfeld ${\displaystyle {\dot {X}}}$ und der Fluss ${\displaystyle X\left(t\right)}$ sind also quellenfrei. Man kann sich die Dynamik im Phasenraum daher als Strömung einer inkompressiblen Flüssigkeit veranschaulichen. Dass das Verschwinden der Divergenz eines Geschwindigkeitsfeldes Inkompressibilität impliziert, lässt sich formal mit Hilfe des Gaußschen Satzes zeigen, ähnlich wie in der Hydrodynamik.

Alternativ und mehr formal ist der Satz von Liouville eine Folge der Invarianz der ${\displaystyle 1}$-Form ${\displaystyle \omega ^{\left(1\right)}=\sum p_{i}\mathrm {d} q_{i}}$ unter symplektischen Transformationen, also auch unter kanonischen Transformationen sowie in der Zeitentwicklung. Damit sind auch die ${\displaystyle 2}$-Form ${\displaystyle \omega =\mathrm {d} \omega ^{\left(1\right)}=\sum \mathrm {d} p_{i}\wedge \mathrm {d} q_{i}}$ sowie ihre Potenzen invariant. ${\displaystyle \omega ^{N}}$ ist das Phasenraumvolumen.

Anwendungen

Der Satz von Liouville spielt implizit eine grundlegende Rolle in der statistischen Mechanik. Es gibt aber auch einfachere Anwendungen.

Teilchenbeschleuniger

Eine Anwendung betrifft die transversale Ausdehnung von Teilchen- oder Lichtstrahlen, etwa in Teilchenbeschleunigern oder optischen Instrumenten. Man kann mit Linsensystemen einen Strahl zwar fokussieren, d. h. seine transversale Ausdehnung verkleinern, das geht aber nur auf Kosten der transversalen Impulse. Die Ausdehnung der transversalen Impulse muss sich so vergrößern, dass das Gesamtvolumen, d. h. das Produkt der Ausdehnung im Orts- und Impulsraum, konstant bleibt. Die Bezeichnung für das entsprechende Phasenraumvolumen in der geometrischen Optik ist Etendue.

Ideales Gas

Ein anderes Beispiel ist ein einatomiges ideales Gas mit Volumen ${\displaystyle V}$ und absoluter Temperatur ${\displaystyle T}$. Die Temperatur ist proportional zur kinetischen Energie der Teilchen, der Teilchenimpuls ist im Mittel daher proportional zu ${\displaystyle T^{1/2}}$. Bei adiabatischer Kompression bleibt laut Satz von Liouville das Phasenraumvolumen, also das Produkt ${\displaystyle VT^{3/2}}$ konstant (im idealen Gas sind die Teilchen voneinander unabhängig).

In einem mehratomigen Gas hat ein Gasmolekül Translations-, Rotations- und Schwingungsfreiheitsgrade. Es sei ${\displaystyle f}$ die Zahl der in der Hamiltonionfunktion quadratisch auftretenden Impulse oder Koordinaten. Bei einem Gas aus zweiatomigen Molekülen ist ${\displaystyle f=3_{\mathrm {trans} } 2_{\mathrm {rot} } 2_{\mathrm {osz} }=7}$. Laut Gleichverteilungssatz hat jede dieser Variablen einen Mittelwert proportional zu ${\displaystyle T^{1/2}}$. Das Phasenraumvolumen eines Teilchens ist dann proportional zu ${\displaystyle VT^{f/2}}$ (Rotations-Koordinaten sind zyklisch und haben konstante Ausdehnung ${\displaystyle 2\pi }$). Bei adiabatischer Kompression bleibt ${\displaystyle VT^{f/2}}$ konstant. Wegen der Quantenmechanik sind die Schwingungsfreiheitsgrade allerdings erst bei sehr hohen Temperaturen (ab etwa ${\displaystyle 2000\mathrm {K} }$) angeregt, und es ist eher ${\displaystyle f=5}$. Bei niedrigen Temperaturen tragen auch die Rotationsfreiheitsgrade nicht mehr bei und es ist ${\displaystyle f\cong 3}$.

Literatur

• Franz Schwabl: Statistische Mechanik. Springer 2006, ISBN 978-3-540-31095-2
• Theodore Frankel: The Geometry of Physics. Cambridge University Press 2012, ISBN 978-1-107-60260-1

Siehe auch

• Satz von Liouville (Funktionentheorie)
• Satz von Liouville (Differentialgeometrie)